zeitform Internet Dienste

Verschlüsselung

Für die technisch Interessierten möchten wir hier gerne einen kleinen Überblick zum Thema Verschlüsselung zeigen. Diese Informationen sind keineswegs vollständig, bieten aber sicher dem einen oder anderen Anhaltspunkte für eine weitere Vertiefung.

Sollten Sie Fragen oder Ergänzungen haben, die auf diesen Seiten nicht erläutert werden, so bedienen Sie sich bitte unseres Formulars.

Bitte beachten Sie, dass diese Seite zu Ihrer freien Verfügung steht und gemäß der GNU Free Documentation License verwendet werden kann. (Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License Version 1.1.).

Was ist Verschlüsselung und woher kommt sie
Alice und Bob - Kryptographische Begriffe
Symmetrische Verschlüsselung
Asymmetrische Verschlüsselung
Empfohlene Literatur und Links

Was ist Verschlüsselung und woher kommt sie

Als Verschlüsselung bezeichnet man ein Verfahren, bei dem mittels eines Schlüssels aus einem Klartext ein Geheimtext (Chiffretext) generiert wird. Das soll anhand eines einfachen Verschlüsselungsverfahrens demonstriert werden:

Angenommen, wir wollen die Nachricht »DIES IST EINE GEHEIMBOTSCHAFT« (Klartext) verschlüsseln und wählen dazu ein Verfahren, bei dem jeder Buchstabe des Klartexts durch genau einen Buchstaben im Geheimtext dargestellt wird. Wir benutzen zu diesem Zwecke folgenden Schlüssel:

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
B C D E F G H I J K L M N O P Q R S T U V W X Y Z A

Alle A des Klartexts werden also durch ein B im Geheimtext ersetzt, alle B durch C usf. Damit lautet unsere neue Nachricht: »EJFT JTU FJOF HFIFJNCPUTDIBGU« (Geheimtext).

Das Verschlüsselungsverfahren ist in diesem Falle die Anweisung, jeden Buchstaben des Klartext durch genau einem Buchstaben im Geheimtext ersetzen. Der Schlüssel lautet in diesem Falle »B«, da alle A durch B ersetzt werden, alle B durch C usf.

Man wird leicht einsehen, dass diese Geheimbotschaft auch ohne Schlüssel leicht zu knacken ist. Beispielsweise kommt das F im Geheimtext sehr häufig vor, was darauf schließen läßt, dass damit ein Buchstabe bezeichnet wird, der auch im Klartext häufig zu finden ist. Wenn man davon ausgeht, dass der Klartext in deutscher Sprache abgefaßt wurde, liegt die Vermutung nahe, dass es sich bei dem F um ein E handelt.

Diese und ähnliche sprachstatistische Überlegungen sind wichtiger Bestandteil der Kryptoanalyse. Natürlich lassen sich solche Auszählungen mit Hilfe eines Computers sehr viel effizienter durchführen und darauf mag sich auch die Meinung mancher Laien gründen, dass jeder Geheimtext prinzipiell zu entschlüsseln sei. Dass das nicht wahr ist, zeigt folgender Geheimtext:

KKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKKK

Verwundert? Einige werden anführen, dass es sich bei dem obigen »Text« gar nicht um einen Geheimtext handelt, da überhaupt keine Nachricht darin verborgen sein kann. Schließlich gibt es keine Sprache, in der der Buchstabe K (oder irgend ein anderer Buchstabe) 33 mal hintereinander vorkommt und doch behaupten wir, dass sich darin eine Botschaft verbirgt. Der Trick ist simpel. Es wird einfach eine neue Chiffre auf jeden neuen Buchstaben des Klartextes angewendet (einmal ersetze ich ein A durch ein B, dann durch ein G oder ein P). Solche Chiffren erhält man, wenn man die beiden oben gezeigten Alphabete gegeneinander verschiebt. Im obigen Beispiel (das in nahezu identischer Form auf den amerikanischen Schriftsteller und Hobbykryptologen Edgar Allen Poe zurückgeht) ist die Bedeutung der Nachricht fast vollständig vom Geheimtext auf den Schlüssel übergegangen. Deshalb ist die Nachricht nicht zu dechiffrieren.

Die Kryptologie ist so alt, wie die Sprache selbst. Fast jede Kultur hat Kryptologie in der einen oder andern Form betrieben. Dabei sind grundsätzlich zwei Motive zu beobachten. Einerseits gibt es die Suche nach dem Schlüssel, der uns den »Geheimtext« der uns umgebenden Natur entschlüsselt. Kabbalisten, Wortmagier und Alchemisten versuchten und versuchen die Welt, die sich als Ansammlung rätselhafter Zeichen darstellt, zu entwirren und die wahre, verborgene Bedeutung hinter dem Schleier der Wirklichkeit zu erkennen. Andererseits wohnt dem Menschen die Lust am Geheimnis, die Lust zur Verschleierung inne und spielt neben den praktischen Gründen für Geheimhaltung (man denke nur an das Militärwesen) eine gewichtige Rolle bei der Entwicklung der Kryptographie.

Dass die Kryptographie eine lange Tradition hat, wird auch an dem oben erwähnten Beispiel deutlich. Es handelt sich dabei um eine sogenannte cäsarische Chiffre; cäsarisch deshalb, weil sie zuweilen von römischen Kaisern benutzt wurde (die im Beispiel verwendete Chiffre wird Kaiser Augustus zugeschrieben). Es handelt sich dabei übrigens um eine echte Chiffre, nicht um einen Code (zwei Begriffe, die in diesem Zusammenhang häufig durcheinander gebracht werden). Die Symbole eines Codes repräsentieren Begriffe (z.B. repräsentiert das Symbol »49« in einer Zeitreihendatenbank den Begriff Deutschland, auch sind alle Arten von Pictogrammen Codes) während die Symbole einer Chiffre Zeichen (in unserem Falle Buchstaben) repräsentieren.

Die erste Veröffentlichung zum Thema Kryptographie stammt übrigens aus dem Jahre 1518 von dem Benediktinermönch Johannes Trithemius. Der »Polygraphiae« – so der Titel des Werks – folgte einige Jahre später das Buch »Steganographiae«, welches u.a. eine ebenfalls sehr alte Sonderform der Verschlüsselung beschreibt: die Steganographie. Hierbei wird der Klartext in einen anderen Text (oder ein Bild etc.) eingebettet und somit gewissenmaßen versteckt. Bekannteste Formen der Steganographie sind das Akrostichon, das Mesostichon und das Telestichon, bei denen jeweils der Anfang (Buchstabe, Silbe oder Wort), der Mittelteil bzw., das Ende eines Verses/Absatz zusammengelesen eine neue Bedeutung ergeben. Besonders im Barock waren diese »Rätsel« (Kryptogramme genannt) ein beliebtes Gesellschaftsspiel. Steganograhische Verfahren kommt in der computergestützten Verschlüsselung – gerade in Zusammenhang mit geplanten gesetzlichen Kontrollen der Kryptograhie – eine zunehmende Bedeutung zu. Mittlerweile sind eine Reihe kommerzieller und Freeware-Programme verfügbar, die die Einbettung beliebiger Dateien in Bitmap- oder Audio-Dateien gestattet.

100 Jahre nach Erscheinen der Werke des Johannes Trithemius wurden diese von der Inquisition als ketzerische Zauberbücher verbrannt. Doch nicht alleine die Inquisition oder andere (staatliche) Repressionen trieben die Kryptologen der Vergangenheit in die Abgeschiedenheit. Kryptologie und Kryptographie galten in nicht wenigen Kulturen als »Wortmagie« und erzeugten Furcht beim einfachen Volk, das Klientel der Kryptographen legte verstärkten Wert auf Verschwiegenheit und Geheimhaltung von Verschlüsselnungsverfahren und schließlich gab es nur bei einem kleinen Teil der Bevölkerung einen Bedarf an Verschlüsselung. Warum dies heute nicht mehr der Fall ist, soll nachfolgend kurz dargelegt werden.

Mit der Entwicklung des Computers entstand die Möglichkeit, Texte in maschinenlesbarer Form zu produzieren. Diese Texte unterscheiden sind qualitativ von einem handschriftlichen Text, da sie einerseits eine eindeutige Identifizierung des Autors nicht zulassen, andererseits einfach und schnell (z.B. nach Schlüsselwörtern) durchsucht werden können. Für handschriftlichen Nachrichten, etwa im persönlichen Schriftverkehr, besteht normalerweise bei Privatpersonen (oder auch Firmen) keine Notwenigkeit zur Verschlüsselung (diese wäre ohnehin sehr aufwendig), da hier die Geheimhaltung durch entsprechende organisatorische Methoden (Post, Kurierdienste) in der Regel gewährleistet und staatlich verankert (Briefgeheimnis) ist. Maschinenlesbare Texte werden zum überwiegenden Teil nicht mit Hilfe von Boten verschickt, sondern über entsprechende Datennetze, die in einem großen Teile der Fälle keinen sicheren Nachrichtenkanal darstellen. Außerdem ist eine Verschlüsselung maschinenlesbarer Texte wesentlich einfacher und schneller zu realisieren.

Daraus folgt, dass mit dem Übergang von handschriftlicher zu elektronischer Kommunikation (z.B. via E-Mail) auch für Privatpersonen, Firmen im zivilen Bereich und staatliche Institutionen, die nicht mit militärischen oder geheimdienstlichen Aufgaben betraut sind, die Notwendigkeit zur effektiven Verschlüsselung von Nachrichten und eindeutiger Identifizierbarkeit des Absenders entsteht. Das bedeutet, dass der Bedarf an leistungsfähigen und einfach implemetierbaren Kryptographieverfahren wächst. Dies zeigt sich unter anderem am Selbstverständnis von Kryptologen, deren Arbeitsgebiet mittlerweile eine anerkannte Wissenschaft ist, die zu Erkenntnissen kommt, die auch in zivilen Bereichen von Nutzen sind. Mit zunehmender Verbreitung von elektronischer Kommunikation im privaten Bereich findet zugleich eine Sensibilisierung der Öffentlichkeit für den Problemkreis rund um Verschlüsselungsverfahren statt.

Alice und Bob - Kryptographische Begriffe

In der kryptographischen Literatur ist es üblich, eine Reihe von Fachbegriffen und Namenskonventionen zu verwenden, die gelegentlich missverständlich gebraucht oder ungenügend verstanden werden. Wir wollen daher zunächst einmal einige dieser Begriffe nennen und erläutern. Und wir wollen Ihnen auch Alice und Bob vorstellen.

Alice und Bob: in der Krypto-Literatur ist oft von Personen die Rede, die Nachrichten an andere Personen schicken und nicht wollen, dass wieder andere Personen diese Nachrichten lesen. Der Einfachheit halber bekommen diese Personen Namen, deren Anfangsbuchstaben nach dem Alphabet sortiert werden. In anderen Worten: es ist einfacher zu sagen »Alice schickt eine Nachricht an Bob« als »Person A schickt eine Nachricht an Person B« (und es klingt netter, wie Carol und Dave finden).

Klartext (plaintext): dieser Begriff kennzeichnet jede Art von unverschlüsselter Nachricht. Der Klartext einer Nachricht ist für jeden lesbar, sein Format (ASCII oder OpenOffice-Dokument) spielt keine Rolle. Er wird in der Regel mit »M« (message) oder »P« (plaintext) abgekürzt.

Chiffretext (ciphertext): dieser Begriff kennzeichnet jede Art von verschlüsselter Nachricht. Der Chiffretext einer Nachricht ist im Normalfall nur von demjenigen lesbar, der den Schlüssel und das Verschlüsselungsverfahren kennt (im anderen Fall ist die Verschlüsselung wertlos). Die Abkürzung lautet in der Regel »C« (ciphertext).

Ver- und Entschlüsselung: sind die Bezeichnungen für die Umwandlung von Klartext in Chiffretext und umgekehrt. Die werden in der Regel mit »E« (encryption) und »D« (decryption) abgekürzt. Für mathematisch begabte Menschen läßt sich dies in zwei Zeilen ausdrücken:

E(M) = C
D(C) = M

Kryptographie, Kryptoanalyse, Kryptologie: während sich die Kryptographie damit beschäftigt, Nachrichten sicher zu verschlüsseln, versucht die Kryptoanalyse, den Chiffretext aufzubrechen und lesbar zu machen. Kryptologie ist der mathematische Oberbegriff der beiden gegensätzlichen Wissenschaftszweige.

Geheimhaltung: Alice will sicherstellen, dass nur Bob ihre Nachricht lesen kann.

Authentisierung (neudeutsch auch Authentifizierung): Bob will sicherstellen, dass die Nachricht von Alice verfaßt wurde und nicht von Carol, die sich als Alice ausgibt.

Integrität: Bob will sicherstellen, dass Alice' Nachricht nicht von Carol verändert wurde, ohne dass er es merkt.

Verbindlichkeit: Alice darf später nicht leugnen können, eine Nachricht gesendet zu haben.

Algorithmus und Schlüssel: mit Algorithmus oder Chiffrierung wird die mathematische Funktion bezeichnet, die zur Ver- und Entschlüsselung eingesetzt wird. Von einem »guten« Algorithmus wird verlangt, dass er durch Kryptoanalyse nicht aufgebrochen oder umgangen werden kann. Eine wesentliche Veraussetzung für einen »guten« Algorithmus ist, dass er offengelegt wurde und dass damit vielen Kryptoanalytikern die Chance gegeben wurde ihn auszutesten. Vertrauen Sie niemals auf Kryptosysteme, deren Algorithmus geheim gehalten wird.

Der Schüssel, abgekürzt mit »K« (key), meist eine beliebige Zeichenfolge aus einem umfangreichen Wertebereich, wird in den Algorithmus eingespeist um den Klartext zu verschlüsseln oder den Chiffretext zu entschlüsseln.

Symmetrische Verschlüsselung

Unter dem Oberbegriff »symmetrische Verschlüsselung« werden alle Kryptosysteme zusammengefaßt, bei denen zur Verschlüsselung und zur Entschlüsselung derselbe Schlüssel verwendet wird. Alice und Bob teilen den Schlüssel als gemeinsames Geheimnis. Sollte Carol Kenntnis von diesem Schlüssel erhalten, kann auch sie den Chiffretext entschlüsseln. Hierin und in der Schwierigkeit, wie Alice und Bob den gemeinsamen Schüssel vereinbaren, ohne dass Carol davon erfährt, liegen die hauptsächlichen Nachteile symmetrischer Verschlüsselungsverfahren.

Dennoch sind symmetrische Verschlüsselungsverfahren nicht überflüssig, eher das Gegenteil ist der Fall. Denn im Gegensatz zu asymmetrischen Verfahren haben sie einen entscheidenden Geschwindigkeitsvorteil. Leistungsfähige Implementierungen symmetrischer Verfahren bieten so hohe Übertragungsgeschwindigkeiten, daß sich damit Sprache und Videokonferenzdaten in Echtzeit verschlüsseln lassen.

In der Praxis werden symmetrische Verschlüsselungsverfahren zur Datenverschlüsselung eingesetzt, während der symmetrische Schlüssel durch asymmetrische Verfahren gesichert übertragen wird (PGP, SSL/TLS, u.a.).

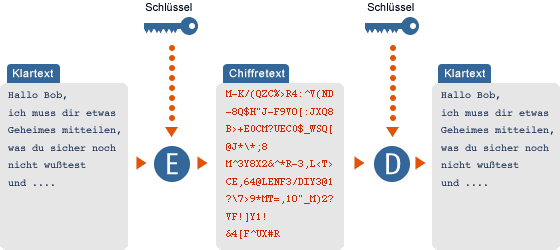
Beispiele für symmetrische Verschlüsselungsverfahren sind:

Federal Data Encryption Standard (DES): Bei DES handelt es sich um ein blockorientiertes symmetrisches Verschlüsselungsverfahren. Es wurde 1974 von der US Regierung vorgestellt und von der ANSI normiert.

DES arbeitet mit einer Schlüssellänge von 64 Bit, wovon jedoch nur 56 Bit signifikant sind. Aufgrund dieser kurzen Schlüsselgröße ist DES eigentlich nicht mehr zeitgemäß und durchaus anfällig für brute force attacks (das systematische Ausprobieren aller möglichen Schlüssel). Auch die US Regierung vertraut nicht auf DES.

Trotzdem hat DES eine weite Verbreitung gefunden und wird insbesondere in Finanz-Applikationen eingesetzt. Etwas neueren Datums ist Triple-DES (3DES), eine DES-Variante, die mit erhöhter Schlüssellänge und Mehrfachverschlüsselung (z.B. 3DES-EDE) arbeitet.

International Data Encryption Algorithm (IDEA): Dieses symmetrische Verschlüsselungsverfahren wurde von J. L. Massey und X. Lai an der ETH Zürich entwickelt und 1990 zunächst unter dem Namen Improved Proposed Encryption Standard (IPES) veröffentlicht. IDEA arbeitet mit 64 Bit Blöcken und verwendet 128 Bit Schlüssel und gilt als sicher. Der Algorithmus hielt bereits umfangreichen kryptoanalytischen Angriffen stand.

Das Patent für IDEA wird von der Ascom Systec AG (Schweiz) gehalten, die nicht-kommerzielle Nutzung ist frei. IDEA kann u.a. von PGP zur Verschlüsselung des Klartextes benutzt werden.

Advanced Encryption Standard (AES/Rijndael): Anfang 2001 veröffentlichte das Computer Security Resource Center des NIST (National Institute of Standards and Technology) einen Vorschlag, den künftigen Verschlüsselungsstandard AES auf dem Algorithmus Rijndael zu implementieren. Seit dem 04.12.2001 hat das NIST AES offiziell als Standard anerkannt und damit die Ablösung von DES eingeleitet.

Rijndael ist ein symmetrischer Blockchiffre für 128-bit-Blöcke mit Schlüssellängen von 128, 192 und 256 Bits.

RC4: RC4 ist ein Stromchiffre (jedes Zeichen wird einzeln verschlüsselt) und wurde 1987 von Ron Rivest für RSA Data Security entwickelt und als »trade secret« geheimgehalten. 1994 wurde der RC4 Algorithmus anonym im Internet veröffentlicht.

RC4 verwendet Schlüssel mit variabler Länge zwischen 1 und 2048 bits und wird in vielen kommerziellen Software-Packeten eingesetzt (z.B. Lotus Notes, Oracle Secure SQL), aber z.B. auch in SSL/TLS-Implementierungen (z.B. OpenSSL).

Stromchiffren gelten als unsicher, wenn ein Schlüssel mehrfach zur Verschlüsselung eingesetzt wird (Software-Implementierungen berücksichtigen dies durch die einmalige Verwendung zufälliger Schlüssel).

Solitaire: Der von Bruce Schneier entwickelte und in Neal Steavensons Buch »Cryptonomicon« vorgestellte Stromchiffre Solitaire realisiert ein Verschlüsselungssystem mit Hilfe eines Bridge Kartenspiels und ermöglicht so (neben Implementierungen in C, Perl und anderen Programmiersprachen) eine manuelle Verschlüsselung von (kurzen) Texten. Selbst wenn man dies nur als interessante Spielerei betrachtet, ist Solitaire ein funktionstüchtiges und interessantes System (allerdings mit in der Vergangenheit entdeckten Sicherheitsproblemen).

Als kleine Spielerei können Sie eine Reihe von symmetrischen Verschlüsselungsalgorithmen (Blockchiffren im CBC-Modus) auf unserer Demo-Seite ausprobieren.

Asymmetrische Verschlüsselung

1976 stellten Whitfield Diffie und Martin Hellman das Konzept der asymmetrischen Verschlüsselung vor. Asymmetrische Verfahren benutzen Schlüsselpaare. Jeder Kommunikationsteilnehmer erzeugt ein solches Schlüsselpaar, das aus einem geheimen Schlüssel (private key) und einem öffentlichen Schlüssel (public key) besteht. In einem asymmetrischen Kryptosystem kann nun eine Nachricht mit Hilfe eines public key verschlüsselt werden. Diese Nachricht kann anschließend nur mit dem dazugehörigen private key wieder entschlüsselt werden.

Ein Beipiel: Alice möchte eine geheime Nachricht an Bob schicken. Dazu schreibt sie diese Nachricht und verschlüsselt sie mit Bobs public key. Anschließend schickt sie die verschlüsselte Nachricht an Bob. Dieser muß nun seinen private key benutzen, um wieder den Klartext zu erhalten.

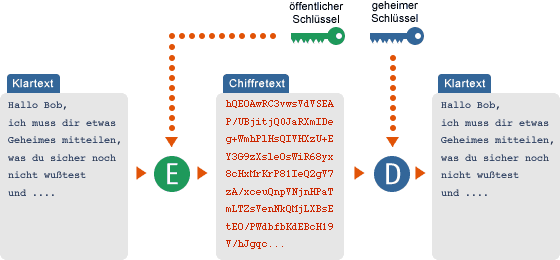
Voraussetzung für das Funktionieren des Verfahrens ist, dass der Absender über den public key des Empfängers verfügt. Da mit Hilfe des public key keine zuvor mit diesem verschlüsselte Nachricht entschlüsselt werden kann, ist die Veröffentlichung des public key bedenkenlos möglich und auch der eigentliche Sinn dieses Schlüssels (Die Veröffentlichung kann beispielsweise über eine Online-Datenbank, einen sogenannten »key server«, realisiert werden).

Der verständige Leser wird gemerkt haben, dass es hier möglicherweise einen Haken gibt. Public key und private key können nicht völlig unabhängig voneinander sein, schließlich bezieht sich eine private key Operation auf eine zuvor durchgeführte public key Operation. Wäre es also nicht möglich aus dem (bekannten) public key den entsprechneden private key zu generieren?

Theoretisch ja. Praktisch ist dies derzeit auch bei vergleichsweise einfachen (sprich kurzen) Schlüsseln nur mit ungeheurem Rechnenaufwand möglich und auch dann nur in einer Zeitspanne, die Monate, Jahre oder auch ein Menschenalter um ein vielfaches übersteigt. Man benötigt dazu mathematische Funktionen (sog. one-way functions), die (derzeit) nur mit extrem hohen Rechenaufwand umkehrbar sind. Wichtig ist, dass es für die Umkehrung der Rechenoperation eine sog. trap door gibt, d.h. eine Information mit deren Hilfe die Umkehrung überhaupt kein Problem mehr ist (in diesem Falle spricht man von trap-door one-way functions). Ein weniger komplexes Beispiele läßt sich auch daheim mit einem billigen Taschenrechner (oder dem eigenen Kopf) nachvollziehen:

Die Multiplikation der beiden Primzahlen 997 und 787 stellt (auch ohne Taschenrechner) nicht wirklich ein Problem dar. Das Ergebnis lautet 784639. Die Umkehrung dieser Funktion bedeutet allerdings (auch mit Taschenrechner) einen erheblich höheren Rechenaufwand. In diesem Falle müßte man die Zahl 784639 in ihre Faktoren zerlegen und das Ergebnis würde 997 und 787 lauten. Tatsächlich basiert die Mehrzahl der heute eingesetzten Public-Key-Systeme auf dem Problem der Primzahlen-Faktorisierung großer Zahlen.

Asymmetrische Verschlüsselungsverfahren sind weniger schnell als symmetrische. Das ist auch ihr entscheidender Nachteil. Das Geschwindigkeitsproblem läßt sich jedoch relativ einfach lösen: Man verwendet einfach eine Kombination von symmetrischen und asymmetrischen Verfahren (Hybridverschlüsselung). In der Praxis wird dazu der Klartext mit einem (schnellen) symmetrischen Verfahren verschlüsselt. Anschließend wird der Schlüssel (der in der Regel wesentlich kleiner ist, als die Nachricht selbst) mit einem asymmetrischen Verfahren verschlüsselt und an die Nachricht angehängt. Der Empfänger muß nun zunächst mit Hilfe des asymmetrischen Verfahrens den Schlüssel entschlüsseln, mit dessen Hilfe er anschließend die eigentliche Nachricht entschlüsseln kann. Das asymmetrische Verfahren dient hierbei also lediglich zur sicheren Übertragung der Schlüsseln für das symmetrische Verfahren.

Dreht man das Verfahren der asymmetrischen Verschlüsselung herum, also verwendet Alice zum Verschlüsseln ihrer Nachricht an Bob ihren geheimen Schlüssel, dann erhält man einen Mechanismus zur Authentisierung und Integritätsprüfung: Bob kann wie jeder andere auch, der Alice' öffentlichen Schlüssel kennt, ihre Nachricht entschlüsseln und lesen, sie ist also keineswegs geheim. Bob kann aber sicher sein, dass die Nachricht tatsächlich von Alice kommt, denn nur sie kann die Botschaft mit ihrem private key verschlüsselt haben, und auch dass die Nachricht nicht von Carol verändert wurde.

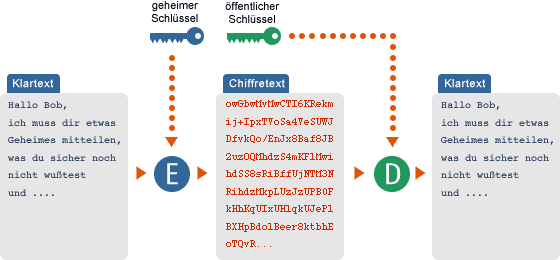
In der Praxis nennt man diesen Vorgang »digitales Signieren« und verschüsselt nicht die gesamte Nachricht, sondern eine daraus gewonnene Prüfsumme (»Digest« oder »MAC – Message Authentication Code«). Diese Prüfsumme wird an die Nachricht angehängt und kann vom Empfänger mit der Prüfsumme verglichen werden, die er mit Hilfe des öffentlichen Schlüssels und der eigentlichen Nachricht erzeugt. Bei gängigen Verfahren zur Prüfsummenbildung (z.B. MD5, SHA-1) wird davon ausgegangen, dass es einem Angreifer nicht möglich ist, die Nachricht so zu verändern, dass sie danach noch mit der Prüfsumme übereinstimmt.

Für diese Authentikationssysteme gelten im wesentlichen die gleichen Vor- und Nachteile wie für die Geheimhaltung: das Schlüsselhandling ist problemlos, aber die Geschwindigkeit ist niedriger als bei symmetrischen Verfahren. Allerdings spielt bei Authentikationssystemen noch ein weiterer Aspekt eine wichtige Rolle: Zwar kann die Integrität einer Nachricht auch mit symmetrischen Verfahren sichergestellt werden, die Authentizität jedoch nur zwischen den Kommunikationspartnern, nicht jedoch gegenüber Dritten.

Ein Beispiel: Alice bestellt für ihre Firma »Alice' Eisenwaren« mit Hilfe einer verschlüsselten Nachricht bei Dave von »Daves Erz-Import« 20 Tonnen Roheisen. Dabei wir ein symmetrisches Authentikationssystem verwendet. Dave ist sicher, dass die Nachricht von Alice kommt, da die Prüfsumme stimmt und Alice zu deren Generierung den gemeinsamen geheimen Schlüssel verwendet haben muß. Er kauft daraufhin Roheisen, um es an Alice zu liefern.

Diese hatte sich aber ursprünglich verkalkuliert und benötigt nun gar kein Eisen mehr, weshalb sie die bald darauf folgende Lieferung nicht annimmt und dreist behauptet, nie eine Bestellung aufgegeben zu haben. Dave wiederum wendet sich an ein Gericht und legt die verschlüsselte Nachricht als Beweis vor. Warum wird der Richter diesen nicht anerkennen?

Nun, da ein symmetrisches Authentikationssystem verwendet wurde, kann Dave die Prüfsumme mit Hilfe der Nachricht und des geheimen Schlüssels, der ja auch ihm bekannt ist, selbst erzeugt und damit die Nachricht gefälscht haben.

Eine solche Situation kann bei der Verwendung asymmetrischer Authentikationssysteme (auch digitale Signatursysteme genannt) nicht entstehen. Hier wird die Prüfsumme mit dem private key des Absenders verschlüsselt. Bei der Entschlüsselung mit dem entsprechenden public key des Absenders kann also einerseits sichergestellt werden, dass die Nachricht nicht geändert wurde (d.h. die Prüfsummen stimmen überein), anderseits ist die Authentizität gewährleistet, da die Prüfsumme nur vom Absender mit seinem (nur ihm bekannten) private key erzeugt werden konnte. Digitale Unterschriften dieser Art werden nach dem Signaturgesetz (SigG) (nähere Informationen) mitterweile auch von deutschen Gerichten akzeptiert.

Beispiele für asymmetrische Verschlüsselungs- und Prüfsummenverfahren sind:

RSA: Das nach seinen Entwicklern R. L. Rivest, A. Shamir und L. M. Adleman benannte Kryptosystem ist z.Z. das bedeutendste asymmetrische Verschlüsselungsverfahren. Es basiert auf dem Faktorisierungsproblem und ist (was sehr wichtig ist) das am besten untersuchte asymmetrische Verfahren überhaupt. Der Algorithmus wurde in zahlreichen Anwendungen implementiert und gilt als sehr sicher. Das Patent wird von RSA Data Security gehalten und ist im Jahr 2000 abgelaufen.

ElGamal: Dieses asymmetrische Kryptosystem (nach seinem Entwickler T. ElGamal benannt) basiert auf dem diskreten Logarithmus Problem. Es gilt in bezug auf die Sicherheit als gleichwertig mit RSA, arbeitet jedoch langsamer und produziert umfangreichere Geheimtexte.

Digital Signature Algorithm (DSA): 1991 wurde DSA vom NIST für den Einsatz im Digital Signature Standard (DSS) vorgeschlagen. Mit DSA ist nur eine digitale Signatur, allerdings keine Verschlüsselung möglich. Die Frage, warum Regierungsstellen einen solchen (sign-only) Standard (z.B. gegenüber RSA) favorisieren, bleibt der Fantasie des Lesers überlassen. Ab 1024 Bit langen Schlüseln gilt DSA als sicher.

Message Digest (MD2, MD4, MD5): Die von R. Rivest für RSA Data Security, Inc. entwickelten Hash-Algorithmen MD2, MD4 und MD5 sind für digitale Signatursysteme gedacht und bilden eine Nachricht beliebiger Länge auf ein »Destillat« fester Länge ab (man spricht in diesem Zusammenhang auch vom digitalen Fingerabdruck einer Nachricht.).

MD2 gilt als sicher, ist aber langsam. MD4 hingegen hat bekannte Schwächen, weswegen von einer Verwendung abgesehen werden sollte. MD5 dagegen gilt als (relativ) sicher und ist sehr weit verbreitet.

Secure Hash Standard (SHA-1): Der vom NIST als Standard verabschiedete SHA-1 generiert 160-bit lange Fingerabdrücke. Er basiert auf den Prinzipien von MD4 und stellt zum gegenwärtigen Zeitpunkt den vermutlich sichersten Hashalgorithmus dar. Wegen potentieller Attacken gegen MD5 sollte zur Berechnung kryptographischer Prüfsummen ausschließlich SHA-1 verwendet werden.

Empfohlene Literatur und Links

Algorithmen:

Kryptographie:

Sonstiges:

Sie können die oben aufgeführten Bücher durch Anklicken des Links »bei Amazon.de bestellen« direkt bestellen. Bitte beachten Sie dabei, dass Sie uns damit eine Werbeprovision von 7,5% des Verkaufspreises zukommen lassen. Für Sie entstehen keine zusätzlichen Kosten. Vielen Dank.